Templating - Multi-entry Templates

By Justin Alei · January 14, 2021 · Read in 34 minutes.

We’re almost there! We finished off our Single Entry templates for our Homepage, Contact and About pages in the last installment, so let’s dive into our final two sections. So far, we’ve been using a dedicated template for each ‘page’ of our site where each template was only being used to display one single Entry. This makes sense when you have single-page top-level sections, but for our Services and Work sections, we have one main section with several sub-pages with the same fields available to each sub-page. EE Templating allows us to use a single template where we can use what’s in the URL to determine what to show. Let’s dive in!

Step 1: Building the Services Section

The Services section is comprised of 4 pages: one main landing page (Services) and the 3x individual ‘service’ pages (Graphic Design, Web Development, Digital Marketing). Each of these pages still has one single entry for each one - we set up the content for these earlier, so we have 4 Entries in our Services Channel - but we’ll use one template to handle displaying all of them (and any future Service Entries). WE WANT the URL for the landing page to be example.com/services, so just like the About/Contact pages, we need a ‘services’ Template Group with an index.html template.

NOTE: We’ve created new Template Groups a couple of times already, each time using the main menu. This time around, I will introduce the new Jump Menu that’s new in EE6. The Jump Menu is in the top-right of the control panel and is a handy new way to navigate around the Control Panel. It uses fuzzy logic to search through various actions so you can find things really quickly, even if you don’t know where they are in the CP. Let’s use it going forward for all our actions.

Hold CTRL or CMD, then press J on your keyboard to activate the Jump Menu. Start typing and notice the shortcuts in the dropdown change as you type. Type "crea temp" and notice the ‘Create Template Group’ is the first option in the dropdown and it’s highlighted. You can move up and down the items in the dropdown with your arrow keys, but in this case, just hit Enter to go to the ‘New Template Group’ screen: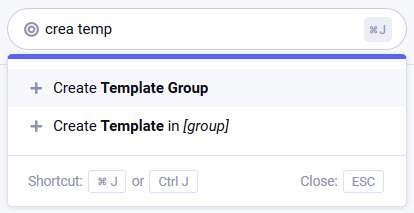
Set the name to services and again, we’ll duplicate an existing group just to get a head-start on our index template - select to duplicate the about group and then save
Open the new services/index template in your text editor and update the channelparameter so channel="services", then head to your browser and go to example.com/services

The Landing Page

The fields available to the Services Channel are the same as the About Channel - and we’ve already build out the Page Builder field template code (being utilized by our {par_page_builder_fluid_field} partial) - so we don’t have to do anything at all within the {exp:channel:entries} tags here… but notice we have a problem! The {exp:channel:entries} tag is set correctly to pull through just one Entry from the Services Channel, but it’s pulling through the wrong one (assuming you created the Services page first then created the sub-pages after like I did). In previous examples, we deliberately only had one Entry in the Channels, but in this case, we have multiples, and by default, the Channel Entries Tag orders the Entries it loops through by the Entry Date field and sorts them ‘descending’ (i.e., newest first). This is really handy for things like news, blog, or portfolio items, but not here.

So we need a way to distinguish the landing page from the other sub-pages. We thought about this in our Content Model planning and when building out our Channels, we created a new Status for this very purpose called "Default Page." So we can use that to identify the landing page:

Back in the services/index template, update the opening Channel Entries Tag to:
```
{exp:channel:entries channel="services" limit="1" status="Default Page"}
```
then save and refresh example.com/services in your browser.

Great, so now our example.com/services page is loading the right Entry, and the page looks good!

The Sub-pages (aka Individual Service Pages)

Now we have our landing page working, but if you go in your browser to example.com/services/graphic-design, you’ll see we still get our services/index template loading (we can tell from the header/footer still displaying), but there’s no Channel content there - the {exp:channel:entries} tag isn’t outputting anything.

NOTE: Thus far, we haven’t paid too much attention to URLs other than to explain the default template routing uses the first ‘segment’ of the URL to establish the Template Group and the second to establish the actual Template. But we’ll be looking at this closer in this section, so it’s important to know in the URL example.com/services/graphic-design, the first segment is services, the second is graphic-design (and so on).

So why isn’t our Channel Entries Tag returning anything anymore? The short answer is because to cater for the landing page above, we added the status parameter that is limiting the output of the tag to only return Entries with the "Default Page" status. But the full answer is worth understanding.

Dynamic URL Segments & Segment Variables

By default, the Channel Entries tag tries to use the information in the URL to establish the right Entry to display. We touched on this earlier when discussing how the dynamic="no" parameter (docs) disables this. Now that we have a second segment in the URL, the default EE template routing is first looking for a template with the name of our second segment (i.e., services.group/graphic-design.html), but that template doesn’t exist… and we don’t want it to exist because don’t want to have to create a totally new template every time we add a Service sub-page. If there isn’t a specific individual template that matches the 2nd segment, then the rendering engine’s next step is to load the index template for the group and use the 2nd segment to try and find an Entry with that segment as the URL Title.

Remember that each Entry has a URL Title which is automatically generated when you enter the Title (and can be overridden if desired)… the exact purpose for this is to be able to use this in URLs and therefore be able to identify individual entries by a specific URL pattern - typically in the 2nd segment. So the resolution to the problem is to only set the status="Default Page" parameter in our {exp:channel:entries} opening tag if we don’t have a second segment - in other words, only if we’re trying to load the Services landing page.

To do this, we can use ExpressionEngine’s URL Segment Variables - these let us grab different segments from the URL and use them in our templates. The typical use for these is exactly what we’re about to do - query it in some way in a conditional and do something based on the result. We can access these with {segment_1}, {segment_2}, and so on in our templates. So to finish this off:

Back in the services/index template, update the opening Channel Entries Tag to:
```
{exp:channel:entries channel="services" limit="1" {if !segment_2}status="Default Page"{/if}}
```
NOTE: When using any kind of variable in a conditional, {if variable_name} and {if !variable_name} are the shortest ways to check if that variable exists or doesn’t exist, respectively.

And that’s it! So our completed services/index Multi-entry template looks like this:

{layout="layouts/_wrapper"}

{exp:channel:entries channel="services" limit="1" {if !segment_2}status="Default Page"{/if}}
  <h1>{if page_heading}{page_heading}{if:else}{title}{/if}</h1>
  {page_intro}
  {par_page_builder_fluid_field}
{/exp:channel:entries}

and through this one template, we’re loading both our Services landing page at example.com/services and all of the sub-pages such as example.com/services/graphic-design. The way we set this up means that any future Entries added to the Services Channel will display using the URL pattern example.com/services/xxxxxxxxxxx where xxxxxxxxxxx is the URL Title of the Entry.

Step 2 - Building the Work Section

We finally made it - this step is what this tutorial is all about! Believe it or not, we’ve already covered a lot of what we need to do, so a good chunk of what we need to do is just re-doing what we’ve already done elsewhere with maybe a few adjustments. So let’s get started.

The Work Landing/Listing Page

Unlike the Services landing page, the Work landing page isn’t actually going to load a single Entry - and it won’t even be editable per se. It’s going to be dynamic in that we’ll be showcasing the Entries from the Work Channel, but it doesn’t have any editable content of its own - it’s just going to be a ‘listings’ page that shows all the portfolio items with links to each individual item’s ‘detail page.’

Note: If you wanted to offer basic editable information, such as an opening introduction paragraph on this page, one option would be to create a Template Variable to hold the text and use that within the otherwise un-editable template.

Back in Part 6, you should have added a bunch of Entries to the Work Channel, so if you haven’t done that yet, go ahead and go back and do that - aim for at least 10 total, have at least one Entry with several images and have at least 4 Entries assigned to one category.

To get started, we again need a new Template Group with an index template:

Use CTRL/CMD + J to activate the Jump Menu, start typing until you find the Create Template Group shortcut, then hit Enter
Set the name to work but don’t duplicate an existing group this time
Open the new work/index template in your text editor, add the same Layout declaration we’ve been using and add an <h1> for the page:
```
{layout="layouts/_wrapper"}

<h1>Our Portfolio</h1>
```
Open up your site/index template and copy the code where we pulled in our 3 latest Work Entries - the concept is identical, we’re just going to adjust a few things.
Paste that code into your work/index template, but remove the dynamic="no" parameter - we’ll cover why later.
Save, then go to example.com/work in your browser.

Your work/index template should now look like this:

{layout="layouts/_wrapper"}

<h1>Our Portfolio</h1>

<div class="row">
  {exp:channel:entries channel="work" limit="3" orderby="date" sort="desc"}
    <div class="col-4">
      <h3><a href="{path='work/{url_title}'}">{title}</a></h3>
      <p><em>{entry_date format="%F %d %Y"}</em></p>
      {work_images limit="1"}
        <img src="{work_images:file}" alt="{work_images:caption}" />
      {/work_images}
      {if client_name}
        <h3>{client_name}</h3>
      {/if}
      <p>{excerpt}</p>
      <p><a href="{path='work/{url_title}'}">Read More ></a></p>
    </div>
  {/exp:channel:entries}
</div>

Notice we have our <h1> tag outside of the Channel Entries loop - this is because we’re using the loop not to output a single page, but to output multiple our Work Entries - just like on the homepage, we’re pulling in ‘visiting content’.

I’ve deliberately left the limit set to 3 for now - limiting the number of Entries returned can be explicit (like how on the Homepage we only wanted 3 Entries to show) or can be used in conjunction with pagination and limit how many are on each paginated ‘page.’ So I’ve left this example with limit="3" so we can cover pagination, but obviously a more realistic limit here is more like 12 or 15 for this type of ‘listing page.’

NOTE: The default limit in a Channel Entries Tag is 100, so if you don’t explicitly set a limit, it will only return up to 100 rows for performance.

Pagination

I’ll assume you’re familiar with the concept of pagination, but if not, read up about it in the docs. Pagination will only display if:

You tell the Channel Entries Tag where to put the paging links with the paginate parameter.

NOTE: The options you’re most likely to use top, bottom or both but note there is also an inline and hidden option - check the docs for more info.
The Channel Entries Tag has more Entries to return than the limit that is set
You include code for the paging links using the {paginate} variable pair

We have a couple options when it comes to adding the code for paging to our templates. Rather than duplicate what’s in the docs, just read this section here then come back. For simplicity, we’re going to use the first option, so:

Back in your work/index template, add paginate="both" as a parameter to the {exp:channel:entries} opening tag
Right before the end of the closing {exp:channel:entries} tag, add the simple {paginate} variable pair. We’ll go ahead and wrap the{pagination_links} single variable with a <div> so you have a way to style it:
```
{paginate}
  <div class="paging">{pagination_links}</div>
{/paginate}
```

Refresh the example.com/work page in your browser and notice that our new ‘paging’ <div> is added both at the top and the bottom but looks kind of weird because it’s inline with all the other ‘col-4’ divs. So the solution here is to not declare our opening and closing ‘row’ divs outside the Channel Entries loop, but rather inside it and use conditionals to display the opening <div> at the top, but only for the first row returned - and the closing <div> at the bottom, but only for the last. Once we do that, our work/index template should look like this:

{layout="layouts/_wrapper"}

<h1>Our Portfolio</h1>

{exp:channel:entries channel="work" limit="3" paginate="both" orderby="date" sort="desc"}
  {if count == 1}<div class="row">{/if}

    <div class="col-4">
      <h3><a href="{path='work/{url_title}'}">{title}</a></h3>
      <p><em>{entry_date format="%F %d %Y"}</em></p>
      {work_images limit="1"}
        <img src="{work_images:file}" alt="{work_images:caption}" />
      {/work_images}
      {if client_name}
        <h3>{client_name}</h3>
      {/if}
      <p>{excerpt}</p>
      <p><a href="{path='work/{url_title}'}">Read More ></a></p>
    </div>

    {paginate}
      <div class="paging">{pagination_links}</div>
    {/paginate}

  {if count == total_results}</div>{/if}
{/exp:channel:entries}

Our Work landing page is now displaying 3 Work entries per page and how many pages you see depend on how many Entries you added. For now, I’m happy with the default output of the {paginate_links} single variable, but like most tags in EE, there are parameters for this tag too that lets you customize how it works - it’s worth taking a look at the docs.

NOTE: You can also set up paging to simply link to the next/previous pages using this code:
{paginate}
  {if previous_page}
    <a href="{auto_path}">Previous Page</a> &nbsp;
  {/if}
  {if next_page}
    <a href="{auto_path}">Next Page</a>
  {/if}
{/paginate}
and if you still want the individual page number links but need more granular control over the HTML output, you can do that too using the {pagination_links} variable pair - check out the docs here.

Notice the pagination works - the URL of each of the ‘page’ links (i.e., for page 2, page 3, etc.) links to the same URL as our main landing page, but with an added ‘pagination segment’ that always starts with a capital P and then a number, where the number represents the number of items for the Channel Entries Tag to ‘offset.’ So in our example, page 2 links to the URL example.com/work/P3 which tells the {exp:channel:entries} tag to skip the first 3 Entries in the loop and start from the 4th.

Now we have pagination working, and our Work landing page is still showing all of the Entries from the Work Channel (albeit only 3 per page). But we also want this landing page to give the user the ability to filter by category. With only a few Entries, it’s not that big of a deal, but imagine there were hundreds, and you can see how being able to filter would be useful.

Work Entry Detail Pages

We’re really close now! The only pages we have left to build out are the individual ‘portfolio detail’ pages where each item from our Work Channel will have its own unique URL and display all our info from our Content Model.

The first thing we need to do is decide our URL and template structure, and we have a couple of options here. Remember the default template routing looks at the first two segments in the URL and uses those to load a specific Template (i.e., segment 2) from a specific Template Group (i.e., segment 1). So if we wanted to, we could utilize a URL structure that looked like example.com/work/entry/sample-project-name and create a new entry.html template within our work.group Template Group to keep the code for our ‘detail’ page in a totally separate template from our ‘listing page’. This is absolutely a legitimate strategy, but I personally prefer a shorter URL, and so I’m going to proceed with the other option which is to use a URL structure like example.com/work/sample-project-name and just continue to use our work/index template making the necessary adjustments for that one template to not only handle the listings but also handle the individual detail pages too. We even already set up the links to the individual Work Entry detail pages for this URL structure when we built out the Homepage (and re-used it above when building out the Work listings page), so we just need to update our work/index template to handle this.

Looking at our Work landing page as it stands now, we’ll go ahead re-use the layout we set up so that each ‘detail’ page also includes the smaller sidebar column with the Category links, but we’ll update the page’s heading so the <h1> is specific to the Work Entry we’re displaying.

So to extend our work/index template to handle ‘detail’ pages, we need to recognize when an individual detail page is being requested. Looking at the URL structure we chose, if the second segment exists, but is neither our special Category URL segment (ie category) nor our paging segment (eg, P3), then we’re trying to load an individual Entry using that Entry’s URL Title. The opening conditional tag to use for this is:

{if segment_2 && segment_2 !="category" && !(segment_2 ~ "/^P\d+/")}

NOTE: In the opening conditional tag above, I’m using the ! and ~ comparison operators in conjunction with parentheses since there is no operator for ‘does not match.’ You can use parentheses in conditionals to group conditions, just like you would with most programming languages. E.g.:
{if (condition_1 && !condition_2) || (condition_1 && condition_3)}

The first thing we’ll do is update our page heading so if we’re looking at an individual Work Entry detail page, we won’t output an <h1>, but instead just a paragraph that’s styled like one. To do this, we’ll just extend the first conditional in the work/index template to also include an {if:elseif ...} tag. We know the first condition will fail because we won’t have category as the second segment and we still want the template to render the <h1> if our new condition checking for a ‘detail’ page fails too, so:

Replace the whole first conditional in the template to:

{if segment_2 == "category" && segment_3}
  {exp:channel:category_heading channel="work"}
    <h1>Our Portfolio: {category_name}</h1>
    {if category_description}
      <p>{category_description}</p>
    {/if}
  {/exp:channel:category_heading}
{if:elseif segment_2 && segment_2 !="category" && !(segment_2 ~ "/^P\d+/")}
  <p class="h1">Our Portfolio</p>
{if:else}
  <h1>Our Portfolio</h1>
{/if}

Next, in the work/index template, add the conditional inside our ‘col-md-9’ div and move the entire {exp:channel:entries} tag to only execute if the condition is not true:

<div class="col-md-9">
  {if segment_2 && segment_2 !="category" && !(segment_2 ~ "/^P\d+/")}
    
    {!-- This is where our 'detail' page code will go! --}

  {if:else}
    
    {exp:channel:entries channel="work" limit="3" paginate="both" orderby="date" sort="desc"}
      {!-- Code stripped for tutorial legibility. Don't change yours! --}
    {/exp:channel:entries}
    
  {/if}
</div>

NOTE: Comments in EE Templates are wrapped with {!-- and --} - anything between these will be completely ignored by the rendering engine.

Inside the conditional, if the condition is true, add a new {exp:channel:entries} tag that will be used to output the individual Entry details. This time, we need to use the url_title parameter and use what’s in the second segment to identify the individual Entry and for output, we’ll just add an <h1> with the Entry Title for now:
```
{if segment_2 && segment_2 !="category" && !(segment_2 ~ "/^P\d+/")}

  {!-- Work Entry detail page --}
  {exp:channel:entries channel="work" limit="1" url_title="{segment_2}"}
    <h1>{title}</h1>
  {/exp:channel:entries}
  
{if:else}
...
```
Now try going to any individual Work Entry’s detail page, e.g.: example.com/work/sample-project-name - you should see the same page layout as our Work landing page, but instead of the multiple Entries being listed in the main column, you should see the Title of your individual entry. And the text "Our Portfolio" should just be a <p> styled to look like a heading 1.

From a templating point of view, that’s pretty much it - this one template now can handle all listings and category-specific listings (both with pagination) and now can also output individual Entry detail pages all by looking at what’s in the URL and acting accordingly!

We just need to finish building out our ‘detail’ page code by adding the rest of the Fields so we can output all our Work Entry data:

Build out the Work Entry detail page {exp:channel:entries} tag, just like we did for the Homepage and Contact page, by systematically going through the Fields available to the Channel and building out each one:
- For the page’s heading, we can re-use the code from the About or Services pages because we’re also using the Page Heading field in our Work Channel:
```
<h1>{if page_heading}{page_heading}{if:else}{title}{/if}</h1>
```
- Client Name is a Text Input field, so needs surrounding HTML if we want to make it a heading, but it’s also not required so we need to check for it first:
```
 {if client_name}<h2>{client_name}</h2>{/if}
```
- Entry Date is one of EE’s default fields an is a Date field, which we can add formatting to:
```
<h3>{entry_date format="%F %d %Y"}</h3>
```
- Project Description is a Rich Text field so has it’s own HTML in the output so we can just drop it in as a single variable:
```
{project_description}
```
- Work Images is File Grid** field that hold multiple images - we’ll display these using a different Bootstrap feature to be different to the Homepage - this time, we’ll output the ‘thumbnail’ Manipulation of our image on the page and link that to the ‘large’ version but inside a Bootstrap Modal:
```
{work_images}
  {if work_images:count == 1}
    <h2>Gallery <small>(click to enlarge)</small></h2>
    <div class="row gallery">
  {/if}
      <a class="col-4" href="#" data-toggle="modal" data-target="#exampleModal">
        <img src="{work_images:file:thumbnail}" alt="{work_images:caption}" />
      </a>
      
      <div class="modal fade" id="exampleModal" tabindex="-1" role="dialog" aria-labelledby="exampleModalLabel" aria-hidden="true">
        <div class="modal-dialog modal-xl">
          <div class="modal-content">
            <div class="modal-header">
              <button type="button" class="close" data-dismiss="modal" aria-label="Close">
                <span aria-hidden="true">&times;</span>
              </button>
            </div>
            <div class="modal-body text-center">
              <img src="{work_images:file:large}" alt="{work_images:caption}" />
              {if work_images:caption}<br /><caption>{work_images:caption}</caption>{/if}
            </div>
          </div>
        </div>
      </div>
  {if work_images:count == work_images:total_rows}
    </div>
  {/if}
{/work_images}
```
- Link is a URL field and again not required. The data held in a URL field is literally just a URL, so we have to add the appropriate surrounding HTML:
```
{if link}<p><a class="button" href="{link}" target="_blank">View the Results</a></p>{/if}
```
- In an individual Entry, you can output any Categories it’s assigned to using the {categories} variable pair within the Channel Entries Tag:
```
<p>
  <strong>Categories: </strong>
  {categories backspace="2"}<a href="{path='work/index'}">{category_name}</a>, {/categories}
</p>
```
  Notice the backspace="2" parameter here - this is a handy parameter available to most EE tag pairs that removes a set number of characters (in this case, 2) from the end of the code only during the last time through the loop. So here we’re adding a comma and space after each category link except for the last one.

Putting all of this together, we have our final work/index template and we are done with our Work section! Here’s our final code:

{layout="layouts/_wrapper"}

{if segment_2 == "category" && segment_3}
  {exp:channel:category_heading channel="work"}
    <h1>Our Portfolio: {category_name}</h1>
    {if category_description}
      <p>{category_description}</p>
    {/if}
  {/exp:channel:category_heading}
{if:elseif segment_2 && segment_2 !="category" && !(segment_2 ~ "/^P\d+/")}
  <p class="h1">Our Portfolio</p>
{if:else}
  <h1>Our Portfolio</h1>
{/if}

<div class="row">
  <div class="col-md-3">
    <h3>Categories</h3>
    {exp:channel:categories show_empty="no"}
      <a href="{path='work/index'}">{category_name}</a>
    {/exp:channel:categories}
  </div>
  <div class="col-md-9">
    {if segment_2 && segment_2 !="category" && !(segment_2 ~ "/^P\d+/")}

      {!-- Work Entry detail page --}
      {exp:channel:entries channel="work" limit="1" url_title="{segment_2}"}
        <h1>{if page_heading}{page_heading}{if:else}{title}{/if}</h1>
        {if client_name}<h2>{client_name}</h2>{/if}
        <h3>{entry_date format="%F %d %Y"}</h3>
        {project_description}
        {work_images}
          {if work_images:count == 1}
            <h2>Gallery <small>(click to enlarge)</small></h2>
            <div class="row gallery">
          {/if}
              <a class="col-4" href="#" data-toggle="modal" data-target="#exampleModal">
                <img src="{work_images:file:thumbnail}" alt="{work_images:caption}" />
              </a>
              
              <div class="modal fade" id="exampleModal" tabindex="-1" role="dialog" aria-labelledby="exampleModalLabel" aria-hidden="true">
                <div class="modal-dialog modal-xl">
                  <div class="modal-content">
                    <div class="modal-header">
                      <button type="button" class="close" data-dismiss="modal" aria-label="Close">
                        <span aria-hidden="true">&times;</span>
                      </button>
                    </div>
                    <div class="modal-body text-center">
                      <img src="{work_images:file:large}" alt="{work_images:caption}" />
                      {if work_images:caption}<br /><caption>{work_images:caption}</caption>{/if}
                    </div>
                  </div>
                </div>
              </div>
          {if work_images:count == work_images:total_rows}
            </div>
          {/if}
        {/work_images}
        {if link}<p><a class="button" href="{link}" target="_blank">View the Results</a></p>{/if}
        <p>
          <strong>Categories: </strong>
          {categories backspace="2"}<a href="{path='work/index'}">{category_name}</a>, {/categories}
        </p>
      {/exp:channel:entries}
      
    {if:else}
    
      {!-- Work landing/listing page --}
      {exp:channel:entries channel="work" limit="3" paginate="both" orderby="date" sort="desc"}
        {if count == 1}<div class="row">{/if}
      
          <div class="col-4">
            <h2><a href="{path='work/{url_title}'}">{title}</a></h2>
            <p><em>{entry_date format="%F %d %Y"}</em></p>
            {work_images limit="1"}
              <img src="{work_images:file}" alt="{work_images:caption}" />
            {/work_images}
            {if client_name}
              <h3>{client_name}</h3>
            {/if}
            <p>{excerpt}</p>
            <p><a href="{path='work/{url_title}'}">Read More ></a></p>
          </div>
      
          {paginate}
            <div class="paging">{pagination_links}</div>
          {/paginate}
      
        {if count == total_results}</div>{/if}
      {/exp:channel:entries}

    {/if}
  </div>
</div>

Again, we’ve deliberately not spent much time on styling, but I trust this tutorial has given you the foundations you need to start building in ExpressionEngine.

What’s Next?

We can still do a few more things to improve our code - things that you’d want to do for a production site, so stick with me for one more chapter.

Justin Alei

Justin is an expert in ExpressionEngine and has created several award-winning sites for Consumer51 on the platform.

Templating - Multi-entry Templates

In This Article:

Step 1: Building the Services Section

The Landing Page

The Sub-pages (aka Individual Service Pages)

Dynamic URL Segments & Segment Variables

Step 2 - Building the Work Section

The Work Landing/Listing Page

Pagination

Categories

Categories Links

Category Headings

Work Entry Detail Pages

What’s Next?

Comments 0